こんにちは、HIKARIです。
中学に入ると部活やスポーツで子どもはどんどん忙しくなってきます。ママも自由になる時間が増えてきてちょっと寂しく感じることもあるのではないでしょうか。
部活動と勉強の両立を応援するべく始めた、「ママが教えるシリーズ」をどうぞよろしくお願いします。
このシリーズではママも一緒に勉強して思い出しながら、子どもに教えれるような解説をしています。目的は授業を楽しく受けれるよう理解をすること、公立高校入試に備えた「これだけはおさえておきたい!」を取りこぼすことなくまとめています。(くれぐれも難関私立高校には対応してませんので、ご理解ください。)
それでは、「乗法と除法」のわかりやすい教え方、ノートのとり方、練習問題を進めていきたいと思います。
集中力を高めるために、100マス計算をしてみよう!
100マス計算 かけ算《PDF》
正の数、負の数の「乗法」とは
乗法の計算について
乗法の計算のポイント
- 同符号の2数の積→絶対値の積に正の符号をつける。(+)×(+)や(-)×(-)→符号は+になる
- 異符号の2数の積→絶対値の積に負の符号をつける。(+)×(-)や(-)×(+)→符号は-をつける
- a×0=0、0×a=0
- a×(-1)=-a、(-1)×a=-a ※-1をかけることは、その数の符号を変えることと同じ

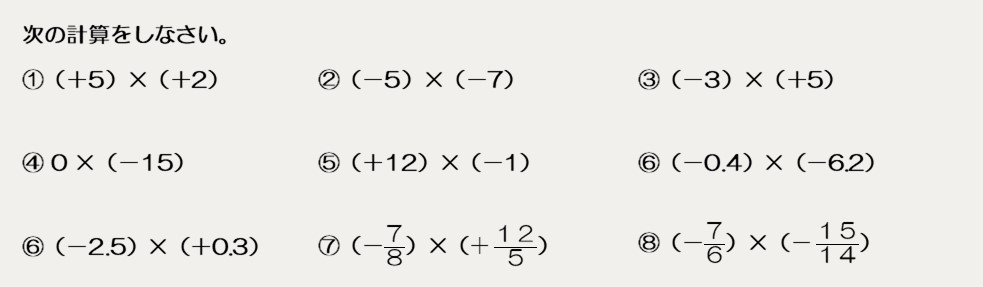
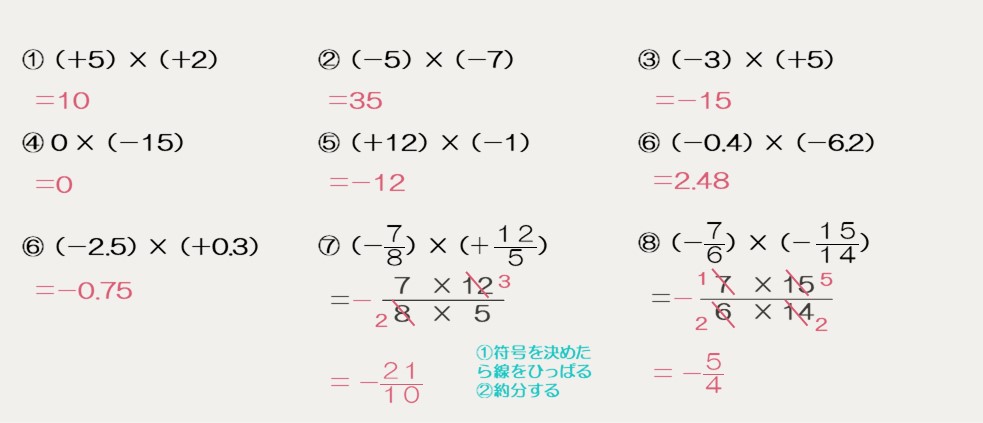
3つ以上の数の乗法について


次の計算をしなさい。

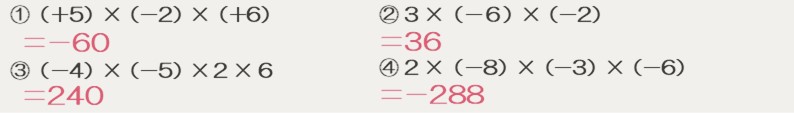
累乗と指数について
 ヒカリ
ヒカリ「素因数分解」で習った累乗と指数について復習しよう!




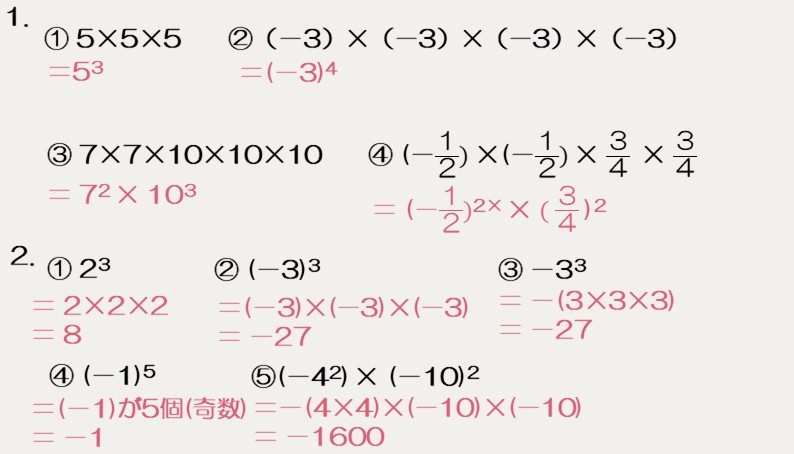
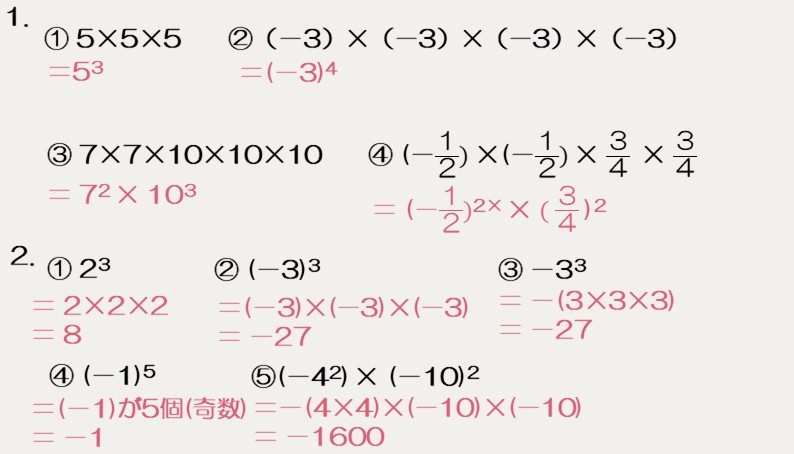
正の数、負の数の「除法」とは
除法の計算について
除法の計算のポイント
- 同符号の2数の商→絶対値の商に正の符号をつける。(+)×(+)や(-)×(-)→符号は+になる
- 異符号の2数の積→絶対値の商に負の符号をつける。(+)×(-)や(-)×(+)→符号は-をつける
- 0をどんな数でわっても商は0になる。0÷a=0 ※どんな数も0で割ることはできない


次の計算をしなさい。
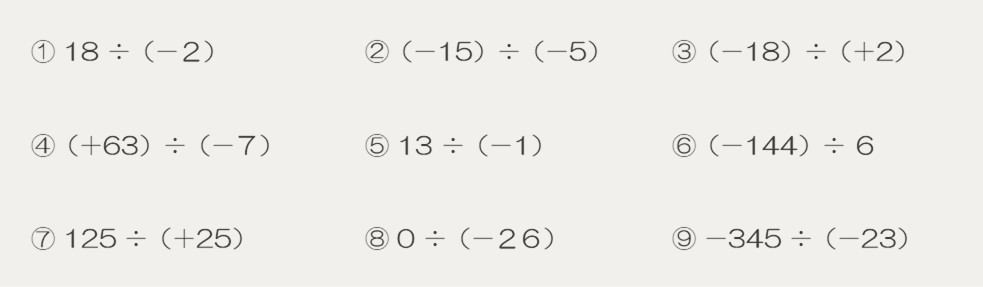
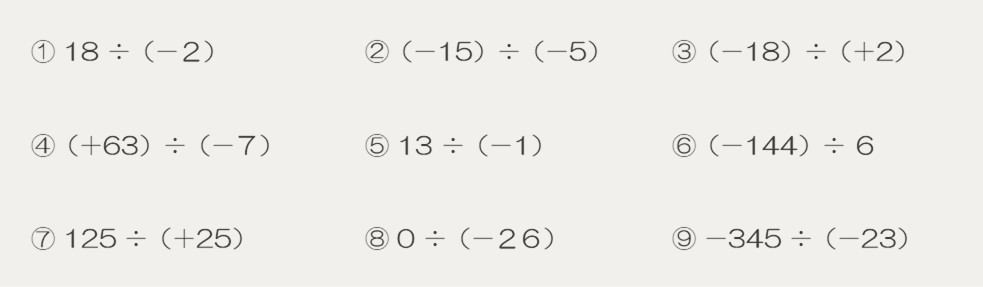
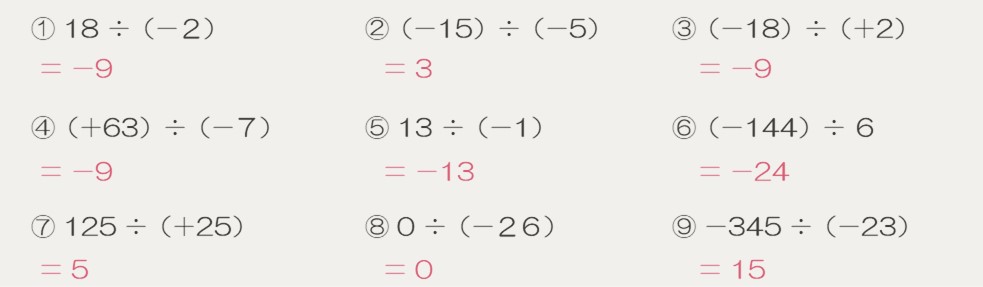
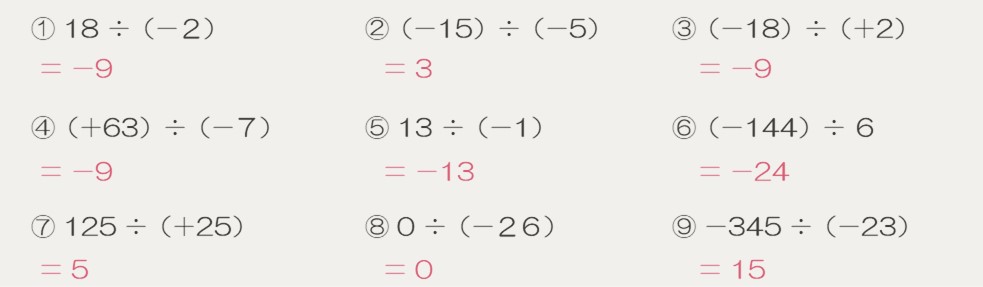
逆数の利用について



分数の逆数を思い出してみて!正負の数のわり算でも逆数を利用して計算するよ。
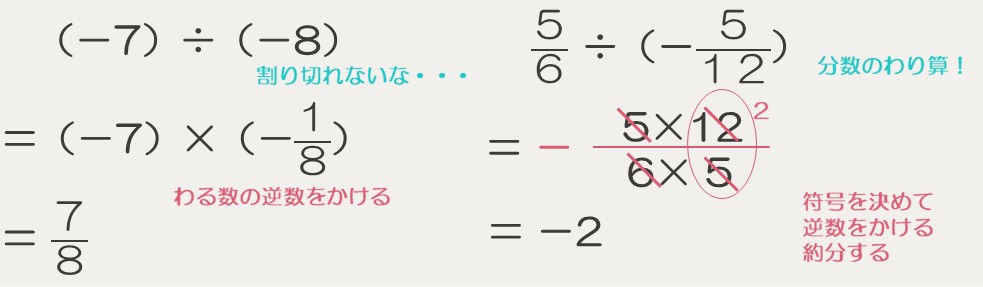
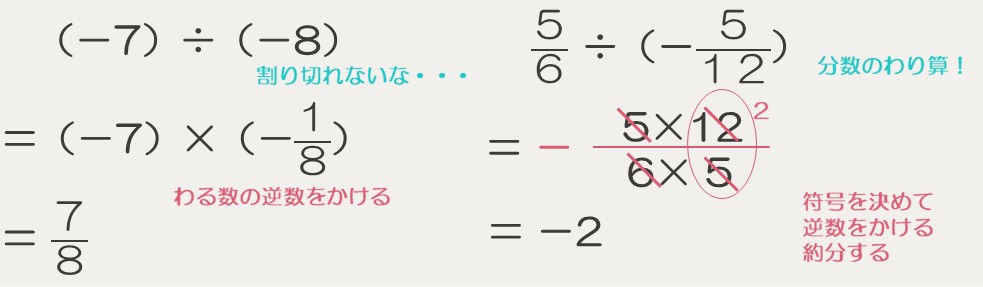
逆数を利用して、次の計算をしなさい。
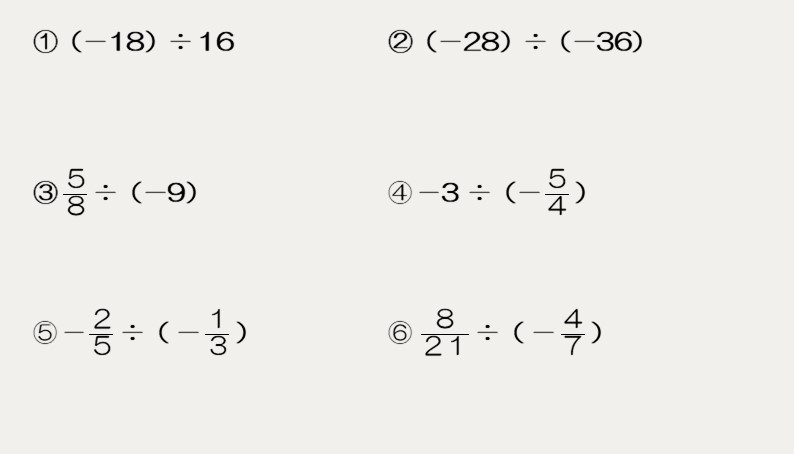
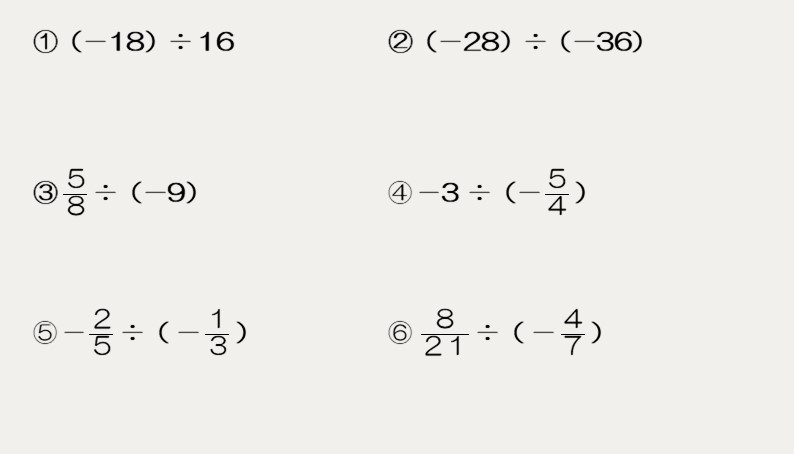
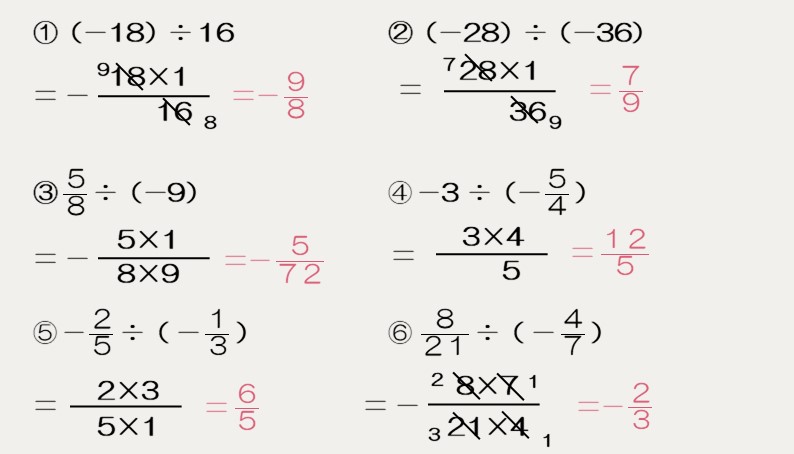
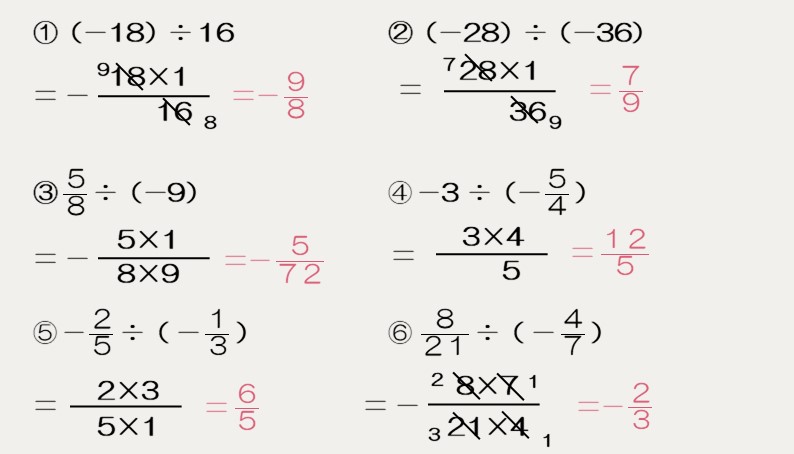
乗除混合の計算
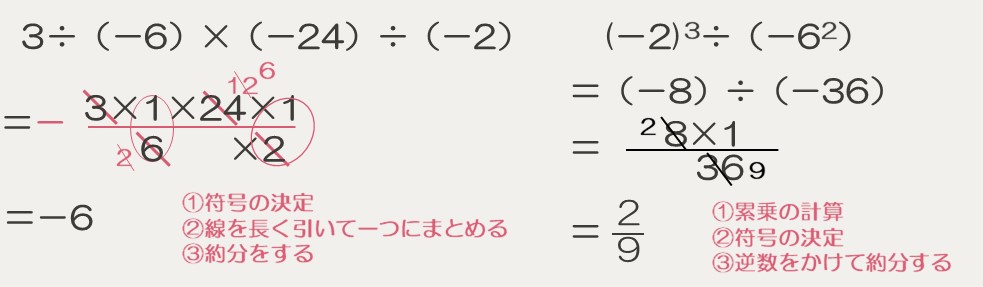
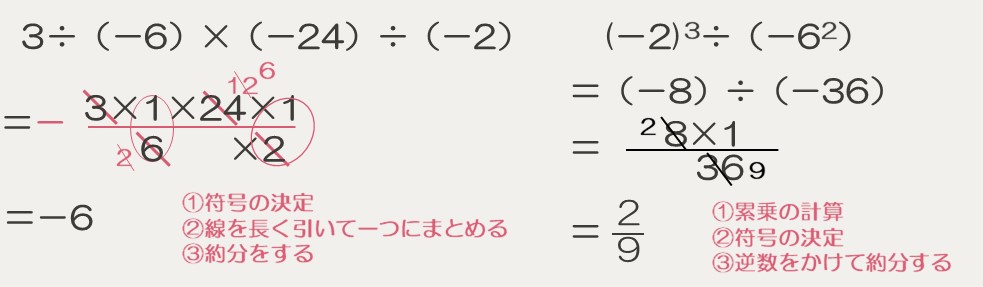
次の計算をしなさい。
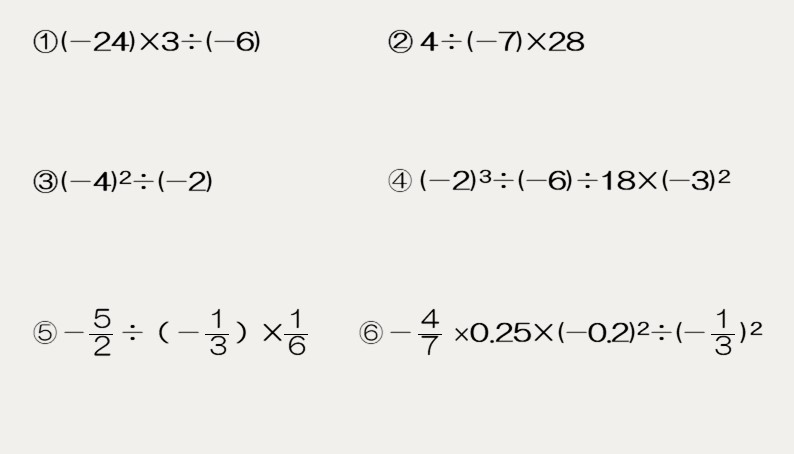
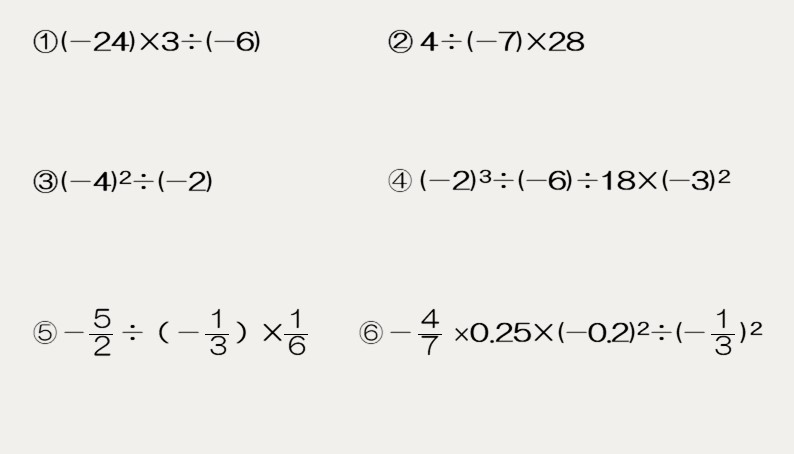
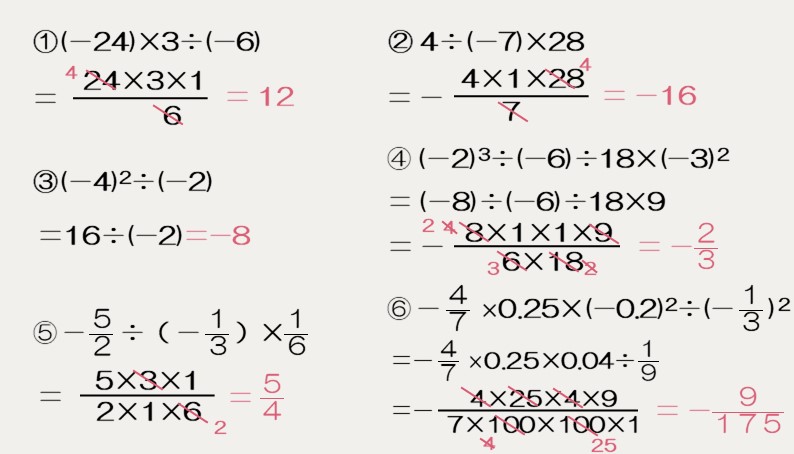
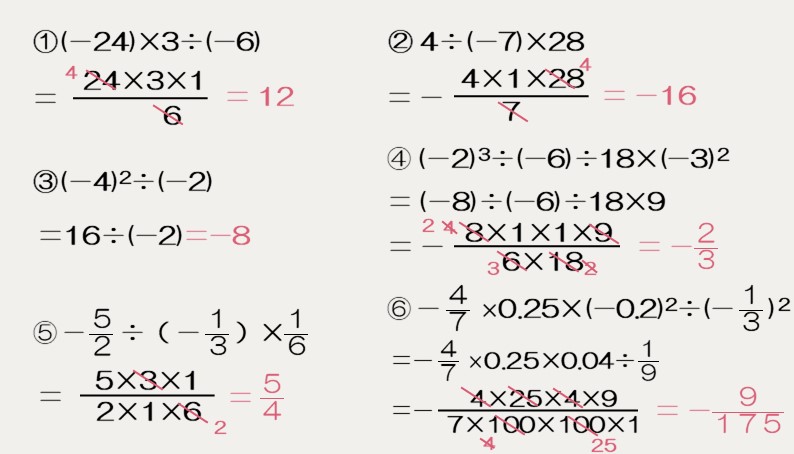
四則混合の計算


次の計算をしなさい。
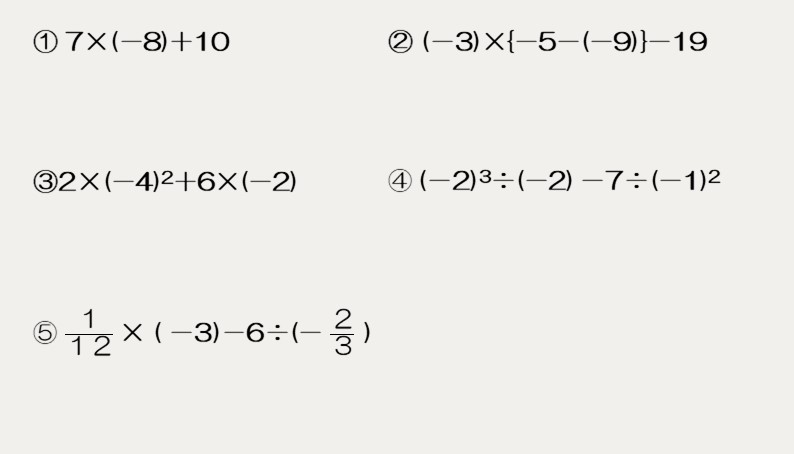
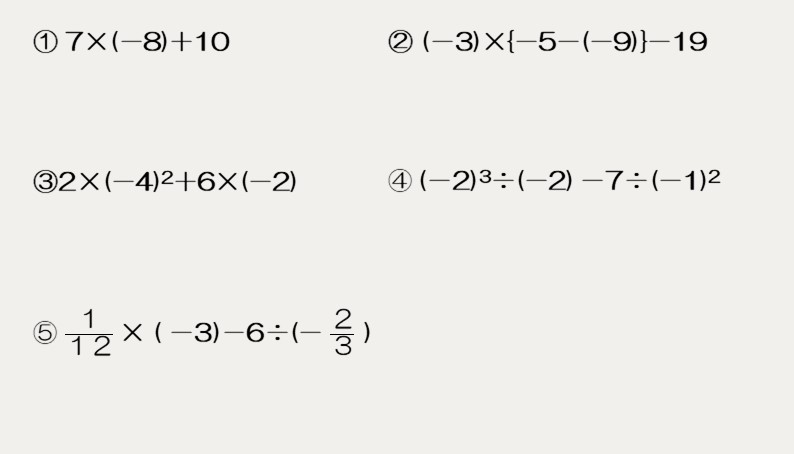
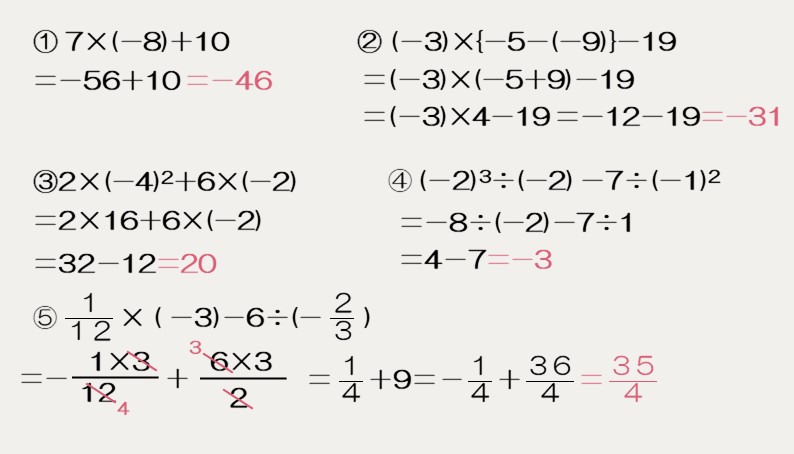
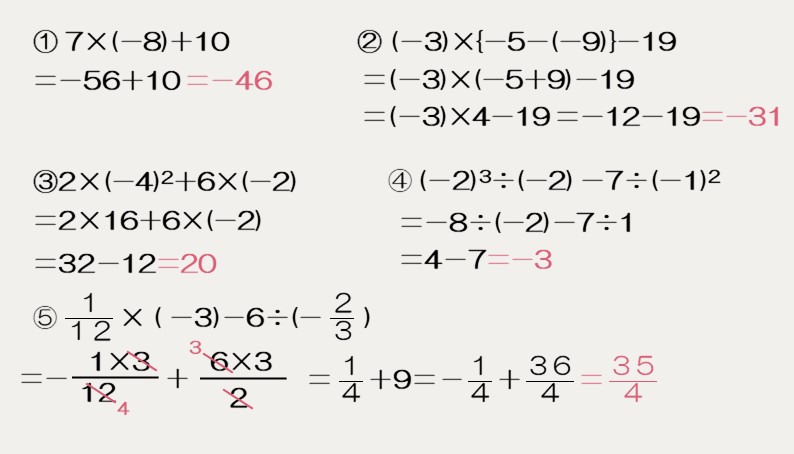
分配法則について





計算の順番としてはかっこ内が先ですが、分配法則を利用すると、計算がカンタンになる場合があります。


ノートのとり方



ノートを見やすくとっておくと、試験のときの見直しにとても役に立つよ!PDFを参考にしてね。
≪参考≫正の数、負の数『乗法と除法』_ノートのとり方(PDF)


まとめ、おすすめ問題集
正の数、負の数の単元が続いていますが、とにかくここではたくさん計算することが大事です。整数、小数、分数、どれでもミスなく正確に計算できるようたくさんの問題を解いていきましょう。
こういった計算問題は入試でも正解率が高い問題です。誰もが正解する問題でミスをしてしまうと、その分難しい問題や他の科目で挽回しなければならなくなります。
着実に正解率を100%に近づけましょう。
正確に計算するためにも、必ず途中式を書くクセをつけましょう。
入試対策問題集など、数学はとにかく解く!解きまくる!!
最後までご覧いただき、ありがとうございました。
次の単元はこちら↓↓↓











コメント