 ヒカリ
ヒカリこんにちは、HIKARIです。
長女、中2後期の学年末テストを終えました。
中2後期の数学といえば、証明問題が中心になってきます。
中学2年の証明では主に、「合同証明」と「合同証明から結論を出す」という問題です。
証明が苦手!という人も、この重要ポイントを丸暗記して、証明のコツさえつかめば点数が取れるようになります!
こちらの記事では、証明問題を解くために頭に入れておかなければいけないポイントをまとめたので活用ください。
目次
証明問題では根拠が必要!
証明問題では材料集めがとても重要になります。
問題の中にある、「・・・ならば」「・・・であるなら」という仮定の他に、図形に関するさまざまな定義、性質、条件を証明の「根拠」として使います。
この「根拠」を覚えないことには、証明問題は解けないので、復習も含め、まとめてみました。
図形の角について
小学生の時に習ったことの復習になります。
覚えているか、確認しましょう。
対頂角の性質
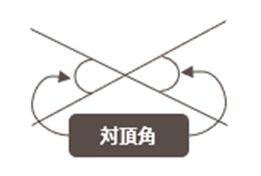

- 対頂角は等しい。
平行線と同位角・錯角
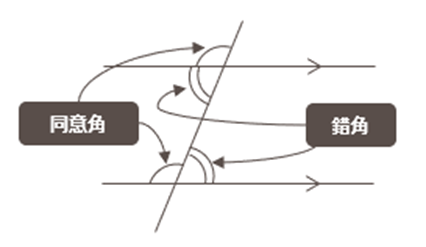

- 平行な2直線に1つの直線が交わるとき、同位角・錯角は等しい。
- 平行な2直線に1つの直線が交わるとき、同位角・錯角は等しい。
三角形の角
- 三角形の内角の和は180°である。
- 三角形の外角は、それと隣り合わない2つの内角の和に等しい。
鋭角・直角・鈍角
- 0°より大きく、90°より小さい角を鋭角、90°の角を直角、90°より大きく180°より小さい角を鈍角という。
三角形の角による分類
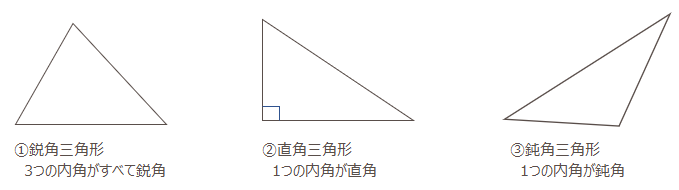

- 鋭角三角形
- 直角三角形
- 鈍角三角形
多角形の内角と外角
- n角形の内角の和は180°×(n-2)である。
- 多角形のの外角の和は360°である。
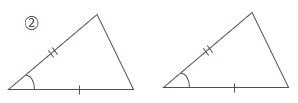
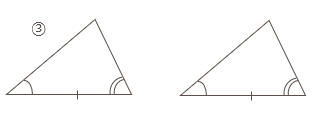
三角形の合同条件
三角形の合同条件
2つの三角形は、次の①~③のうち、どれかが成り立てば合同である。
- 3組の辺がそれぞれ等しい。
- 2組の辺とその間の角がそれぞれ等しい。
- 1組の辺とその両端の角がそれぞれ等しい。
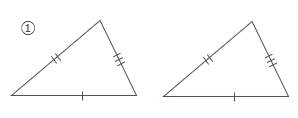



直角三角形の合同条件
2つの直角三角形は、次の①、②のどちらかが成り立てば合同である。
- 斜辺と1つの鋭角がそれぞれ等しい。
- 斜辺と他の1辺がそれぞれ等しい。


三角形の定義と性質
正三角形の定義と性質
- 3つの辺がすべて等しい三角形。(定義)
- 正三角形の角はすべて等しい。
- 正三角形の角はすべて60°である。
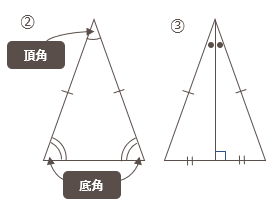
二等辺三角形の定義と性質
- 2つの辺が等しい三角形。(定義)
- 二等辺三角形の底角は等しい。
- 二等辺三角形の頂角の二等分線は、底辺を垂直に2等分する。

平行四辺形
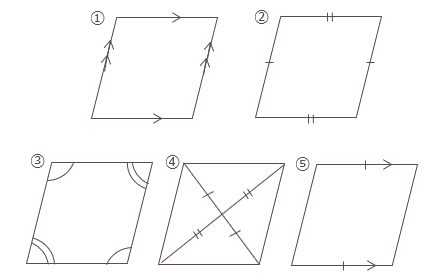
平行四辺形の定義と性質
- 2組の対辺がそれぞれ平行な四角形。(定義)
- 2組の対辺はそれぞれ等しい。
- 2組の対角はそれぞれ等しい。
- 対角線はそれぞれの中点で交わる。
平行四辺形になるための条件
- 2組の対辺がそれぞれ平行である。
- 2組の対辺がそれぞれ等しい。
- 2組の対角がそれぞれ等しい。
- 対角線がそれぞれの中点で交わる。
- 1組の対辺が平行でその長さが等しい。

証明の重要ポイントプリントダウンロード
\これを覚えていれば証明はラク!/
次回は、証明問題を解くコツを解説したいと思います。
最後までご覧いただき、ありがとうございました。









コメント