こんにちは、HIKARIです。
勉強からず～っと離れているママも教えれるよう、わかりやすい説明を心がけながら「ママが教えるシリーズ」をつくりあげたいなと思っています。
ヒカリ疑問やわかりにくいところがあったら気軽にコメントやお問い合わせください♪改善していきたいと思ってます！
さて、先取り学習！
１２月から「中学数学」の勉強に取りかかっています。コツコツと早め早めに進めて、スポーツとの両立を全力でサポートするために今日も母は一緒に勉強していきます。
それでは、『素因数分解』のわかりやすい教え方、ノートのとり方、練習問題を進めていきたいと思います。
ヒカリ『素因数分解』は数学の整数分野の基礎になり、後に習う『平方根』（ルートをつかうやつ！）にも利用します！
しっかりおさえておきましょう！！
【整数について】素因数分解に入る前におさらいしよう！
ヒカリ『素因数分解』に入るまえに、小学5年生でならった整数である『自然数』と『素数』についておさらいしておこう！！
自然数とは・・・１，２，３,…のような、１以上の整数のこと。（0は自然数ではない！）
素数とは・・・２，３，５，７…のように、１とその数以外に約数をもたない自然数のこと。（1は素数ではない！）
- １～２０の自然数で素数をすべて求めよ。
-
STEP1～20までの数字を書き出し、１を消す
１，２，３，４，５，６，７，８，９，１０，１１，１２，１３，１４，１５，１６，１７，１８，１８，２０STEP「2」を残し、2の倍数を消していく１，２，３，４，５，６，７，８，９，１０，１１，１２，１３，１４，１５，１６，１７，１８，１９，２０※2の倍数は下一桁が偶数（0，2，6，8）
STEP「3」を残し、3の倍数を消していく１，２，３，４，５，６，７，８，９，１０，１１，１２，１３，１４，１５，１６，１７，１８，１９，２０※3の倍数は全ての桁の数を足すと3の倍数
- 12→1+2＝3
- 36→3+6＝9
- 111→1+1+1＝3
STEP「５」を残し、5の倍数を消していく（「4」は2の倍数で消えている）１，２，３，４，５，６，７，８，９，１０，１１，１２，１３，１４，１５，１６，１７，１８，１９，２０STEP「7」は実際に割ってみる（「6」は2の倍数で消えている）
上の結果から、２０以下の素数は、
２，３，５，７，１１，１３，１７，１９
２０以上４０以下の素数をすべて求めよ。
《解き方》２０以上４０以下の整数を書き出して上のやり方で消していく。
２０，２１，２２，２３，２４，２５，２６，２７，２８，２９，３０，３１，３２，３３，３４，３５，３６，３７，３８，３９，４０
２３，２９，３１，３７
素因数分解をしていこう！
ヒカリたとえば、『３５』を素因数分解するイメージをしてみよう！
素数のかけ算で表すということは、３５＝５×７になります。
『５』も『７』も素数なので素因数分解をしたことになります。
ヒカリイメージがわいたと思うので、本格的に素因数分解のやり方を説明するよ！
６０を素因数分解せよ。
- 自然数を書く
- 線を引く
- 小さい素数から割っていく
- 素数を×でつなげる
- 指数でまとめる
上のやり方で素因数分解を進めて行きます。
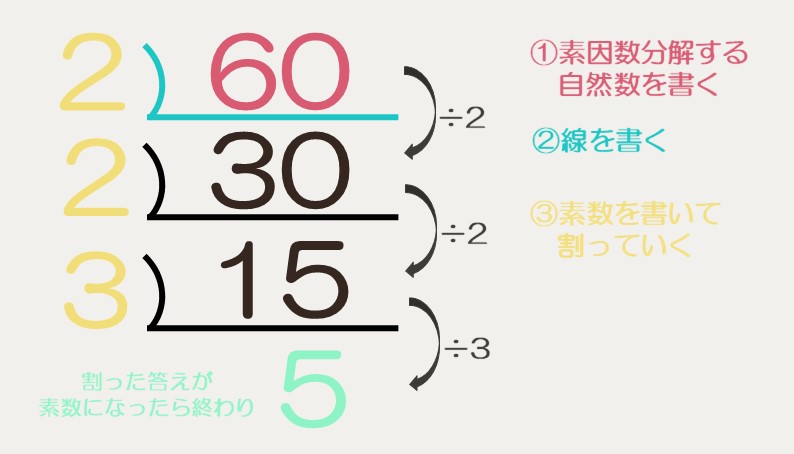
割り算のひっ算が逆さになったような形で「素数」でどんどん割っていきます。最後「素数」になったら終わりです。
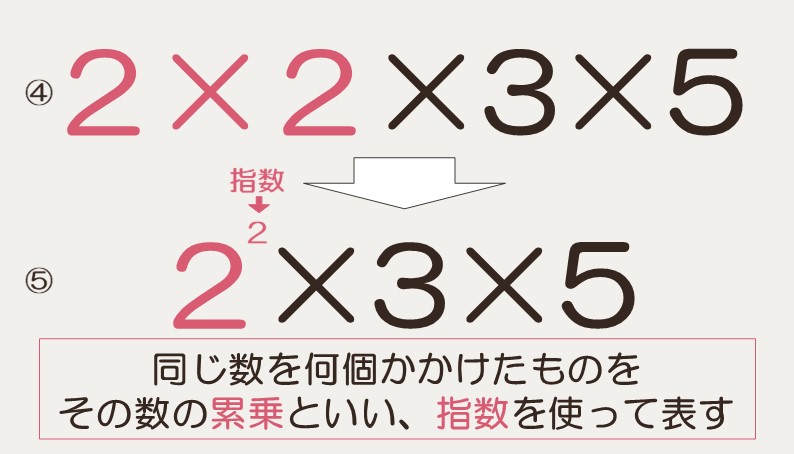
６０を素因数分解すると 22×３×５ となります。（小さい素数から順に書く）
次の数を素因数分解しなさい。
（１）２０ （２）８０ （３）１８０ （４）３１５ （５）５２５
（１）22×５ （２）24×５ （３）22×32×5 （４）32×5×7 （５）3×52×7
素因数分解では、よく「わりきれる素数をみつけられない！」なんてこともよく聞きます。
- 20までの素数（2,3,5,7,9,11,13,19）は頭に入れておき、割ってみる
- 偶数（数字の1の位が0,2,4,6,8,）は2でわれる
- すべての桁の数字をたして、3の倍数であれば3でわれる→例：126＝1+2+6＝9(3の倍数)
- 数字の1の位が0,5の場合は5でわれる
- 7,9,11,13,19・・・とわってみる
素因数分解の利用した問題を解いていこう！
素因数分解と平方
素因数分解を利用して平方の問題を解くことができます。
300にできるだけ小さい自然数をかけて、その結果をある自然数の平方にしたい。どんな数をかければよいか。また、その結果はどんな自然数の平方になるか。
ヒカリこの問題では２つのことを聞かれているので注意！
300＝22×3×52
3だけ2乗（平方）になっていない。したがって、3をかけることで、
22×32×52にすることができる
300に3をかけると22×32×52となるので（2×3×5)2＝302となる
答・・・3をかけると、30に平方になる
次の問いに答えなさい。
（１）50にできるだけ小さい自然数をかけて、その結果をある自然数の平方にしたい。どんな数をかければよいか。また、その結果はどんな自然数の平方になるか。
（２）126にできるだけ小さい自然数をかけて、その結果をある自然数の平方にしたい。どんな数をかければよいか。また、その結果はどんな自然数の平方になるか。
（３）1323をできるだけ小さい自然数でわって、商がある自然数の平方にしたい。どんな数で割ればよいか。また、その結果はどんな自然数の平方になるか。
（１）2をかけると、10の平方になる
50＝2×52→2をかけることで22×52になる→(2×5)2→102
（２）14をかけると、42の平方になる
126＝2×32×7→2×7をかけることで22×32×72になる→(2×3×7)2→422
（３）3で割ると、21の平方になる
この問題は割るので、33に注目！3で割ることで32になる
1323＝33×72→3で割ることで32×72になる→(3×7)2→212
それぞれ確かめ算ができます。
（１）50に2をかけてみる→50×2＝100、10×10＝100
（２）126に14をかけてみる→126×14＝1764、42×42＝1764
（３）1323を3で割ってみる→1323÷3＝441、21×21＝441
平方数を覚えよう！
素因数分解と約数・倍数
（１）上の左の《考え方》を利用して、275の約数をすべて求めなさい。
１、５、１１、２５、５５、２７５
≪解き方≫
275＝52×11
52の約数は1、5、52
11は素数なので約数は1、11
それぞれかけいくと、1×1、1×11、5×1、5×11、52×1、52×11を計算すると約数が求めれる。
素因数分解と最大公約数・最小公倍数
最大公約数とは・・・複数（2つ以上）の正の整数に共通な約数（公約数）のうち、最大の数をさす
最小公倍数とは・・・複数（2つ以上）の正の整数に共通な倍数（公倍数）のうち、最少の数をさす
２４と１２０の最大公約数と最小公倍数を求めなさい。
答・・・最大公約数２４、最小公倍数２４０
（１）次の２数の最大公約数、最小公倍数を求めなさい。
①２４，１８０ ②７２，８８ ③５４，３９６
（２）３つ以上の数の最大公約数、最小公倍数を求めなさい。
①２４，５６，８４ ②３６，６０，９６
（１）①最大公約数・・・１２、最小公倍数・・・３６０
②最大公約数・・・８、最小公倍数・・・７９２
③最大公約数・・・１８、最小公倍数・・・１１８８
（２）①最大公約数・・・４、最小公倍数・・・１６８
②最大公約数・・・１２、最小公倍数・・・１４４０
３つ以上の数の場合は、
最大公約数→すべての数に共通な素因数で割り、すべての数に共通な素因数の積が最大公約数となる。
最小公倍数→２つ以上の数に共通な素因数で割り、割り切れない数はそのまま下におろす。2つ以上に共通な素因数がなくなるまで繰り返す。割った素因数と残った商すべての積が最小公倍数となる。
ノートのとり方
ヒカリ今回勉強したことを、ノートにまとめるとこんな感じになるよ！
PDFを参考にしてね！
≪参考≫整数の性質『素因数分解』_ノートのとり方（PDF）
まとめ、おすすめ問題集
2021年度はちょうど教科書改訂の年になります。
教育出版の年間学習指導計画を元に各章をさらに細かくして学習を進めて行こうと思っています。
数学は問題をたくさん解いて慣れる必要があります。中間テスト、期末テスト対策としては、先生によって問題を出す傾向があるので必ずテスト用紙はわかりやすく保管しておきましょう。（意外と重要です！）
また、ママが教えるシリーズでは各章の「基本」をわかりやすく解説しています。
数学のレベルアップをはかるなら、「基礎⇒標準⇒応用」と問題をレベルアップして解いていく必要があります。
最後までご覧いただき、ありがとうございます。
ヒカリ頑張るあなた、頑張るママを応援します！
／
次の単元はこちら↓↓↓
＼
コメント