 ヒカリ
ヒカリこんにちは、HIKARIです。
円周角の定理をつかった角度を求める問題は入試でよく出されます。
円周角は中3後期で習いますが、入試に出る頻度があまりに高いので夏休みに勉強している人も多いでしょう。
角度を求める問題は、図形の定義・定理の知識も必要ですが、”ひらめき”も大事です。
”ひらめく”ために何が必要かというと、それは『数多く問題を解くこと』です。
入試の数学問題は時間との勝負です。
問題に慣れておくこと、時間をかけず”ひらめく”ために今回は円周角の定理を使った角度を求める問題プリントを作成しました。
円周角の定理の復習と角度を求めるときのコツも合わせて紹介したいと思います!
目次
【円×角度】問題で必ず覚えておきたいこと!
円周角の定理
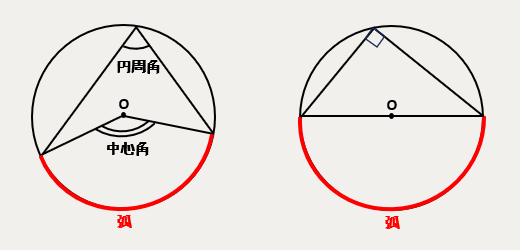

- 1つの弧に対する円周角の大きさは一定であり、その弧に対する中心角の半分である。
- 半円の弧に対する円周角は90°である。



最初はなかなか対応する円周角や中心角を見つけられなかったりしますが、それぞれの角がどの弧に対応するかを考えれば見つけられるよ!
弧と円周角
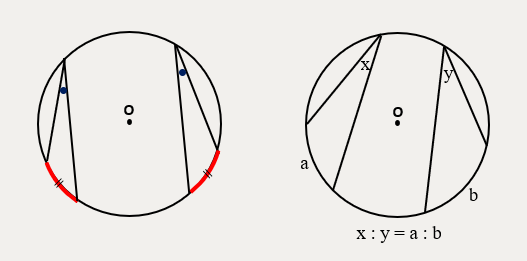

- 1つの円で、等しい長さの弧に対する円周角は等しい。逆も成り立つ。
- 1つの円で、円周角の大きさは弧の長さに比例する。
円に内接する四角形
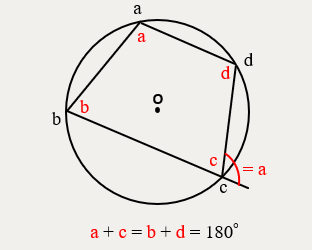

円に四角形が内接する(4つの頂点が円周上にある)とき、
- 1つの対角の和は180°である。
- 外角はそれととなり合う内角の対角に等しい。
二等辺三角形の定義
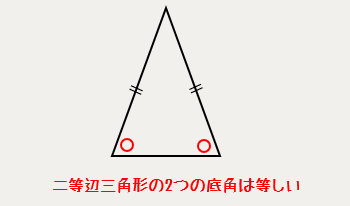




二等辺三角形の底角が等しいという定義は円周角を求める問題でよーく使うので必ず覚えておきましょう!
【円×角度】問題をすばやく解くコツ!
円周角の定理を使った角度を求める問題で意識することは、
- すでにわかっている角度を絡めて、わかる角度を書き込んでいく
- 円周角・中心角に対応する弧を見つける
- 円の直径・半径を意識する
- 補助線を引く
円周角の定理をつかった角度を求める問題・基本編
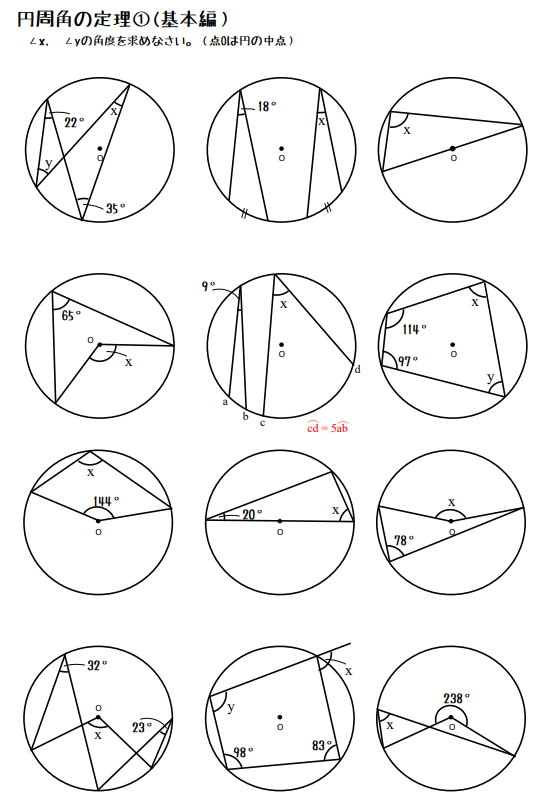

円周角の定理をつかった角度を求める問題・応用編
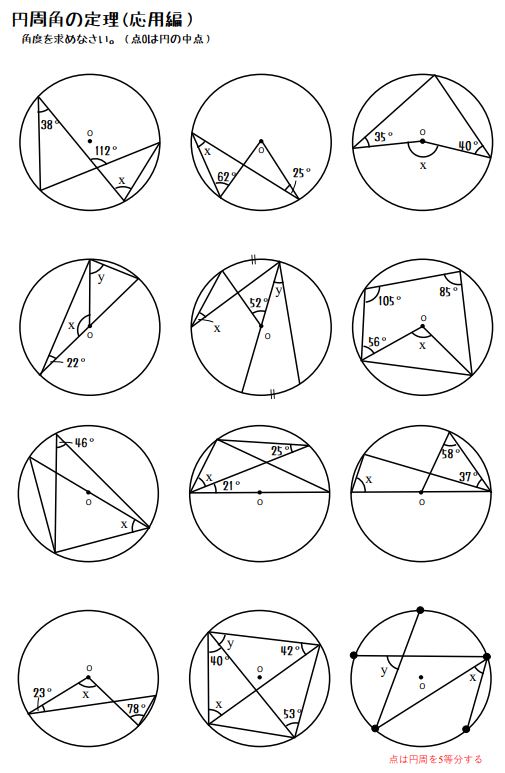

円周角の定理をつかった角度を求める問題・難問編
※2番目の問題→線分BCは円Oの接線です。
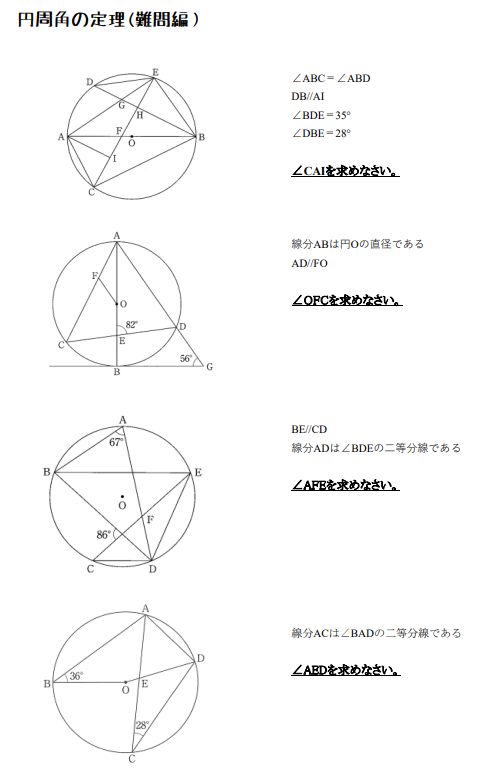

まとめ
入試への出題頻度が高い『円周角』のプリントをご紹介しました。
数学はどの単元も、”たくさん問題を解く!”が大事です。
最後までご覧いただき、ありがとうございました。









コメント
コメント一覧 (2件)
難問編の2問目、接線であるか明記されていなくても解けますでしょうか?
回答が遅くなり申し訳ありません。
コメントありがとうございます!
そして、ご指摘の通り、『円の接線は、接点を通る半径と垂直をなす』を利用しているので明記が必要ですね。
ありがとうございました。